Besoin d'un peu d'aide ?

figure 21

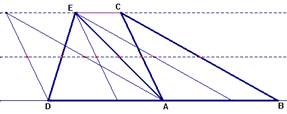
figure 22

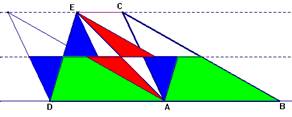
figure 23

Comme certaines (au moins) des pièces communes auront des côtés portés par les côtés des triangles de départ, il paraît opportun de tracer par les sommets de l’un et l’autre triangle des parallèles aux côtés de l’autre, ce qui peut se traduire aussi par des translations amenant certains sommets à coïncider (figure 22).

Par ailleurs, la droite des milieux peut jouer un rôle, ces milieux pouvant être centre de symétrie pour certaines  pièces éléments (figure 23).

Ces deux idées suffisent ici à trouver la décomposition.

La démarche de Gerwien s’appuie sur ces idées simples, mais cherche évidemment à mettre en place une méthode générale et systématique de décomposition de deux ou plusieurs polygones équivalents que nous ne traiterons pas ici.