Autres exemples de problèmes de fermeture:

Les configurations  conduisant à des problèmes de fermeture peuvent varier à l’infini. En voici quelques unes, plutôt élémentaires :

Un exemple classique

Sont donnés: un triangle quelconque ABC et un point M sur l’un de ses côtés. On trace (MN) parallèle à un côté ne contenant pas M, qui rencontre le troisième côté en N. Puis on recommence avec N.

figure 5

Problème 1

Démontrer que la ligne polygonale ainsi obtenue se ferme toujours sur M au bout du sixième segment (sauf un cas particulier où c’est au bout de trois segments)

Situation plus générale

Que se passe-t-il si l’on remplace les trois directions parallèles aux côtés par trois directions quelconques distinctes deux à deux δ, ε, φ ?Peut-il y avoir fermeture ?

Ici la réponse n’est en général pas simple du tout. Elle le devient pourtant si l’on remplace le triangle donné par un cercle.

figure 6

Problème 2

Démontrer que si l’on prend trois directions successives distinctes deux à deux, il y a toujours fermeture avec le sixième segment (exceptionnellement au bout du troisième segment)

figure 7

Problème 3

Démontrer que si l’on prend deux directions faisant un angle α, il y a fermeture au bout d’un nombre fini de segments si et seulement si
α=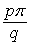  (p et q entiers). Sur la figure 8, , mais vous pouvez faire varier p et q, ainsi que la direction intitiale donnée par B.

figure 8

On peut généraliser ce problème, ainsi :

Problème 4

Si l’on prend n directions (n impair), correspondant aux n côtés d’un polygone inscrit dans un cercle, démontrer que la ligne se ferme en général au bout de 2n segments. (Que se passe-t-il si n est pair ??)

figure 9