Puzzles et équidécomposabilité des polygones plans
La construction des puzzles est une activité ludique autant que formatrice en géométrie, à tous les niveaux d’enseignement. Elle pose aussi des problèmes théoriques de fond qui alimentent encore aujourd’hui la réflexion et la recherche de certains mathématiciens.
L’un des thèmes étudiés concerne ce que l’on désigne du nom un peu savant d’équidécomposabilité des polygones plans qui est en pratique simplement la résolution du problème suivant :
étant donnés plusieurs polygones plans de même aire, les découper chacun selon les mêmes parties triangulaires ou polygonales en nombre fini. En voici un exemple à partir d’un pentagone régulier, un carré et un triangle (figure 1) :
dont une équidécomposabilité globale en 11 morceaux est donnée par la figure 2 :

figure 1
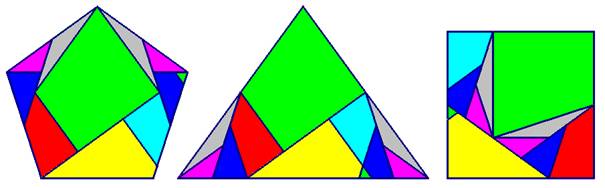
figure 2
vous pouvez voir sur l'animation suivante les opérations permettant de passer de l'une à l'autre figure :
figure 3
figure 4
Dans la pratique, pour déterminer l’équidécomposabilité d’un nombre quelconque de polygones de même aire, il suffit de l’avoir mise en évidence par paire de polygones puis de superposer les décompositions.
Ainsi la décomposition commune des trois polygones de la figure 2 est obtenue par la superposition de deux décompositions du triangle, l’une avec le pentagone (figure 3), l’autre avec le carré (figure 4)
Le principe de la superposition est donné par la figure 5 : la décomposition selon les Ai et celle selon les Bj donnent, en les superposant, une nouvelle décomposition selon les Ck qui contient les deux décompositions précédentes.
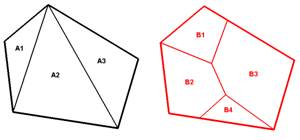
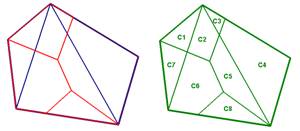
figure 5
figure 5 bis
Les polygones considérés sont dans un plan euclidien et G est un groupe d’isométries de ce plan.
Deux polygones sont pseudo-disjoints si leur intersection est constituée uniquement de segments.
Deux polygones P et Q sont équidécomposables selon le groupe G d’isométries s’il existe un nombre fini de polygones Ai pseudo - disjoints deux à deux, un même nombre de polygones Bj pseudo- disjoints deux à deux et un même nombre d’isométries fk de G telles que
P = UAi ; Q = UBj ; et pour tout i, fi(Ai) = Bi , au besoin après un réarrangement des indices.
Alors, la relation d’équidécomposabilité selon G est une relation d’équivalence (notée quelquefois ≈ dans la suite), ce dont nous laissons au lecteur le soin de le démontrer.
N.B. Dans la suite, lorsque nous parlerons simplement d’équidécomposabilité sans préciser le groupe G, c’est que celui-ci est le groupe des déplacements du plan.


