problèmes en vrac...

Problème 10

Soient deux cercles concentriques de rayons R (pour le cercle extérieur), et r (pour le cercle intérieur).

Démontrer que la ligne polygonale se referme au bout de n tangentes si et seulement si il existe p entier naturel tel que =

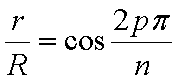
Figure 17

Un exemple ancien en est donné par ce qu’on appelle la relation d’Euler pour un triangle mais qui a été trouvée et démontrée pour la première fois  en 1746 par William Chapple (1711 ? – 1781)

Problème 11

Les cercles (O) et (O’) ont pour rayon respectif R et r, avec (O’) à l’intérieur de (O).

Soit d = OO’ la distance des centres.

A partir d’ un point A sur (O) on trace une tangente au cercle (O’) qui recoupe le cercle (O) en B.

De B on trace la seconde tangente à (O’) qui recoupe (O) en C.

De C on trace une troisième tangente.

Figure 17

Démontrer que la ligne polygonale ABC…se referme en A au bout de la troisième tangente si et seulement si
d² = R² – 2Rr.

Figure 18

Un autre exemple en est donné par le problème 12 qui suit. :

Problème 12

Soient deux cercles (O) et (O’) tels que le premier passe par le centre O’ du second.

Soient [AB], [BC] et [CD] trois cordes du cercle (O) ;

démontrer que si (AB), (BC) et (CD) sont toutes les trois tangentes au cercle (O’), respectivement en a, b, c, il en est de même de la droite (DA).

(Autrement dit la ligne polygonale ABCDX, inscrite dans le cercle (O) et circonscrite au cercle (O’) se referme en A).

Démontrer que (OO’) est un axe de symétrie pour le quadrilatère (ABCD)