Quelques pistes supplémentaires

Les problèmes liés à des polygones inscrits dans un cercle se traitent bien évidemment avec les relations entre mesure de l’angle inscrit et mesure de l’arc intercepté.

Voici un exemple :

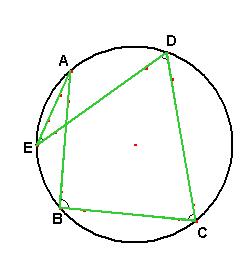
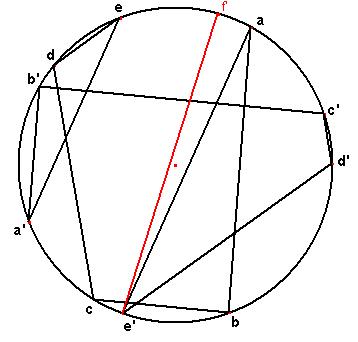
Soit ABCDE la ligne polygonale de référence, et abcdea‘b’c’d’e’f’…la ligne construite par parallélisme. On a 
arc AC + arc BD + arc CE + arc DA + arc EB 
= arc ac + arc bd + arc ce + arc da’ + arc eb’
= arc ab’ + arc ba’ = 2kp,

mais cela ne permet pas d’affirmer que a = a’, mais seulement que (ab) est parallèle à (a’b’) ce que l’on savait déja. Ensuite,

arc AC + arc BD + arc CE + arc DA + arc EB + arc AC
+ arc BD + arc CE + arc DA
= arc BE + 2kp.

De même on a :

arc ac + arc bd + arc ce + arc da’ + arc eb’
+  arc a’c’ + arc b’d’ + arc c’e’ + arc d’f’
= arc af’ + arc be’.

Mais  arc be’ = arc BE donc arc af’ = 2kp

donc f’  est confondu avec a.

Si les arc sont égaux chacun à chacun (arc AC = arc ac ; arc BD = arc bd, etc ) alors les deux lignes polygonales sont homothétiques et la ligne abcdef…se referme en a.

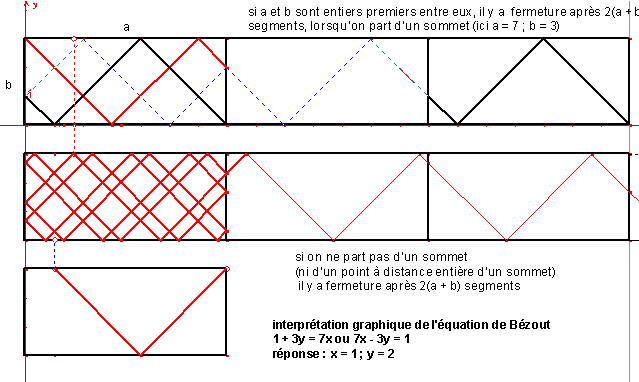
Problème 6

Si les côtés sont mesurés par les entiers a et b (situation à laquelle on peut toujours se ramener lorsque a et b sont commensurables), on cherche le plus petit commun multiple de a et b. En particulier, lorsque a et b sont premiers entre eux, ce PPCM est ab. Voir les figures ci-dessous. (On suppose a > b)

Remarquons  que si a et b sont premiers entre eux, en prenant comme point de départ le point situé à une unité d’un sommet, sur le côté a, on a une illustration de l’équation de Bézout :
ax + by = 1

Pour les problèmes 8 et 9 on cherchera de même le plus petit multiple commun à b.p/q et a.

Problème 10

Repérer les sommets par des angles a₁, a₂, …a_n, a_n+1 = a₁ (s’il y a fermeture) et remarquer :

1) que a_k+1 – a_k est constant pour k entier compris entre 1 et (n – 1) ;

2) que

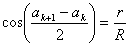
Problème 12

Considérons les symétries axiales par rapport à (O’B), puis (O’C) puis (O’D) :
elles transforment (AB) en (BC)
puis (CD) puis (DX) tangent à (O’, r) et coupant (O, R) en X.

On en déduit l’angle

(AB, DX) = (AB, CD) + (CD, DX) )

= (O’a, O’c) + (O’c, O’d)

= (O’a, O’d)

Mais les points A, B, O’, D sont cocycliques donc
(AB, AD) = (O’B, O’D) )

= (O’a, O’d) = (AB, DX) ;

Donc (AD) = (DX) ou A = X

Problème 13

T étant le point de contact de (AF) avec (O) et φ l’angle COT,
montrer que 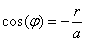et .
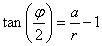Remarque : en posant x = 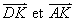= - 1, on est conduit à l’équation x³ – x - 2 = 0.

Problème 14

C’est sans doute le plus difficile et la solution analytique développée ci-dessous n’est peut-être pas la plus élégante. N’hésitez pas à nous en proposer une meilleure.
Désignons par (a, a’), (b, b’) et (c, c’) les coordonnées respectives de A, B et C. En exprimant le fait que la distance de O aux droites (AB), (BC) et (CA) est égale à 1, on obtient les trois relations :

(ab’ – ba’)² = (a – b)² + (a’ – b’)²

(bc’ – cb’)² = (b – c)² + (b’ – c’)²

(ca’ – ac’)² = (c – a)²  + (c’ – a’)²

dans lesquelles  on remplacera a’ par (ua² + v) et des relations analogues pour b’ et c’.

En mettant en évidence les fonctions symétriques de a, b et c on arrive à dégager les relations :

u(ab + bc + ca) = u + 2v 

puis a + b + c + abc = 0

et enfin (u + v)² = 1

Pour l’orthocentre H, les mêmes relations conduisent à
y_H = (u – 1)/u  et  x_H = (a + b + c)(1 – 2u)

lorsque  u + v + 1 = 0 :
y_H = -(u + 1)/u et x_H = (a + b + c) (1 + 2u)

lorsque u + v = 1