Cas de deux rectangles équivalents mais en position quelconque
Pour traiter le cas de deux rectangles équivalents mais en position quelconque, Hadwiger et Glur commencent par démontrer l’équidécomposabilité translative d’un rectangle et d’un parallélogramme de même base, situés entre les mêmes parallèles.
Celle-ci peut être très simple (figure 31) ou plus compliquée (figure 33), selon que la projection orthogonale des côtés obliques sur l’une ou l’autre base tombe à l’intérieur ou à l’extérieur de cette base.
Dans ce second cas (figure 33), on « redressera » de proche en proche le parallélogramme selon le principe de la figure 32.
figure 33
Décomposition qui peut finalement se simplifier en regroupant les polygones identiques et contigus (figure 34) ; ce qui donne une autre idée de décomposition, plus simple, et consistant à découper des tranches parallèles de la largeur du rectangle.
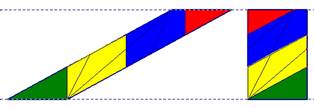
figure 34
3. Puis est étudiée l’équidécomposabilité translative de deux rectangles équivalents quelconques R
et R’. Le principe consiste à utiliser la transitivité en construisant :
1.les parallélogrammes équivalents P et P’, compris entre les mêmes bases que les rectangles,
2. une direction
sur laquelle les bases des rectangles R
et R’ se projettent
selon des segments de même longueur, et sur lesquels on construira des rectangles égaux R1 et R’1 et, bien sûr, équivalents à R
et R’. (figure 35)
Il suffit alors d’appliquer les équivalences R ≈ P ≈ R1 ≈ R’1 ≈ P' ≈ R’, et de les traduire en décompositions géométriques que l’on superpose au fur et à mesure. (figures 36 et 37)
. Alors la direction cherchée, définie par
, est perpendiculaire à
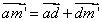puisque
.