D'autres problèmes à explorer

On aura remarqué dans tous ces problèmes, que lorsqu’il y a fermeture, il y aura toujours fermeture quel que soit le point de départ ; et lorsqu’il n’ y a pas fermeture pour un point précis, il ne peut jamais y avoir fermeture pour aucun autre point. Mais on peut rencontrer des situations dans lesquelles il y a fermeture pour certaines positions seulement et pas dans le cas général, comme dans l’exemple qui suit d’un cercle inscrit dans un carré de même centre.

Problème 13

Soit un carré ABCD de centre O, de demi diagonale
OA = a, et (O) un cercle  centré en O et de rayon r inférieur à a.
Les tangentes issues de A au cercle (O) recoupent (BC) et (DC) en E et F.

Démontrer que (EF) est tangente au cercle (O) si et seulement si

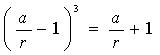
Figure 19

Démontrer que, en dehors des points M pris aux sommets du carré, la ligne polygonale MNPQ, formée par les tangentes successives au cercle (O) ne se referme pas.

Figure 19 bis

remarque : on peut trouver des rayons du cercles pour lesquels elle se referme, mais ce sera un autre rayon que celui calculé précédemment. D'ailleurs, en déplaçant M, on pert cette fermeture.

Le cas de la parabole.

Problème 14

Soit (P) la parabole d’équation y = ux² + v (u non nul)
relativement à un repère orthonormé d’origine O et (O) le cercle centré en O et de rayon 1

D’un point A quelconque de la parabole (P)   on construit une tangente à (O) qui recoupe (P) en un point B .

De B on construit la seconde tangente à (O) qui recoupe (P) en C , et de C on construit une troisième tangente à (O).

Démontrer que cette troisième tangente repasse par A, quel que soit le point A pris au départ. sur (P) si et seulement si
(u + v)² = 1

Démontrer que dans ces conditions, l’orthocentre du triangle ABC se déplace sur une droite fixe lorsque le triangle ABC varie sur la parabole en restant tangent au cercle (O).

Vérifier que ce point est fixe lorsque
u = 1/2 ou lorsque u = - 1/2

problème 14

Ce ne sont là que quelques exemples pour montrer la variété, la richesse et quelquefois la complexité des problèmes de fermeture. Chacun d’entre vous pourra imaginer ses propres situations et proposer ses solutions. A vos règles, stylos et logiciels de dessin !