Une difficulté, surmontée
3. Il y a cependant une difficulté dans ce second cas ; c’est que le point E n’est pas forcément situé entre B et C comme dans la figure 14 (il est alors en K).
Cette dernière situation peut néanmoins se ramener à la précédente, en
accolant des triangles
de même base (en rouge sur la figure) situés entre les même parallèles, jusqu’à aboutir à un triangle débordant le point K.
Il suffit après cela de superposer les deux décompositions obtenues par les procédés 1° et 2°.
figure 14
Déplacez le point C
ajoutez des triangles avec le curseur
Dans la pratique, la figure devient vite complexe par la multiplication rapide du nombre de polygones réalisant la décomposition : voir exemple de multiplication exponentielle des polygones fig 14-bis
C’est pourquoi nous traiterons (figure 15) un exemple ne nécessitant que l’ adjonction d’un triangle pour dépasser l ’intersection de (AD) avec la base (BC) .
Dans ce cas, la décomposition des deux triangles accolés ACH et ABC , d’une part, DCH et DCB d’autre part, par le procédé n° 1 est très simple, rajoutant les milieux I , J , L , M .
Le procédé n° 2 appliqué aux triangles ACH et DCH , rajoute les milieux N et O ainsi que les découpes [KJ] et [KM] .
figure 15
Il faut maintenant encore superposer les deux découpages des triangles ACH et DCH .
Pour cela il suffit d’appliquer
- la symétrie de centre E milieu de [CK] pour les segments contenus dans les triangles symétriques CKN et CKO ,
et
-
les translations de vecteur
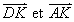, respectivement, pour les segments contenus dans les triangles
KOD
et
KMD
, (respectivement
ANK
et
AJK
).
animation 1
Cela nous donne ici un total de 11 triangles ou polygones pour réaliser l’équidécomposition des triangles ABC et DBC. ( animation 1 (laissez la souris ici) )
Pour cela, il suffit de ramener ces composants dans les triangles ABC et DBC, par translation ou par symétrie centrale, selon la disposition des parties obtenues par le procédé n° 1.
De cette manière le polygone PQRS est envoyé par symétrie dans le triangle ABC, par translation dans CDH et par une nouvelle symétrie dans DBC.
Par contre le triangle JQK est envoyé par translation dans le triangle ABC et dans CDH, puis enfin symétrie dans le triangle DBC.
En effectuant les transformations pour tous les polygones et triangles composants on obtient finalement l’équidécomposabilité des triangles ABC et DBC en 11 éléments, qu’on peut regrouper en six seulement, en regroupant les morceaux qui sont contigus.
animation 2
4. Exercice. Soient donnés deux triangles ABC et ADE de même base et de même hauteur (figure 20). Trouver une ST - décomposition de ces deux triangles en les mêmes morceaux triangulaires ou polygonaux (figure 21).
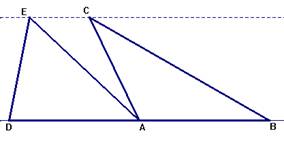
figure 20